Méthode
Ce qui nous vient à l’esprit en premier quand on pense a une carte, c’est une représentation sur papier d’une portion de l’espace, une partie de notre Terre. D’autres formes de cartes peuvent exister, celles d’un monde fictif (comme la Terre du Milieu), des cartes conceptuelles ne représentant pas véritablement un espace mais un réseau, ou encore une schématisation comme le plan du métro parisien: il s’agit bien d’une étendue spatiale mais qui ne respecte pas exactement la réalité de la construction, seule les interconnexions sont considérées.
Nous allons nous intéresser ici à l’exemple le plus naturel de carte:
Représentation d’une portion de la terre sur une feuille.
Nous vivons dans un monde en 3 dimensions, on peut aller en avant, sur le côté et en hauteur. Sur une feuille en revanche, en dessinant, on ne peut aller que de gauche à droite et de haut en bas. Impossible de creuser la feuille ou d’y mettre du relief. Il n’y a que 2 dimensions.
Une “portion de la terre” est en 3 dimensions et une “feuille” est à deux dimensions. La définition d’une carte devient alors:
Représentation d’un objet en 3 dimensions sur un support en 2 dimensions.
Il faut donc trouver un moyen pour faire cette conversion. Tout ce qui nous intéresse en réalisant une carte basique ce sont les deux dimensions longueur et largeur, on n’a pas besoin de la hauteur. Un immeuble sera représenté par sa longueur et largeur à sa base, et on va omettre sa hauteur. De même la hauteur d’une montagne ou la profondeur d’un océan ne seront pas affichés dans un premier temps. Ils le seront par d’autres moyen, à l’aide de couleurs et de symboles.
Tout aurait été simple si l’on avait été dans l’antiquité à considérer que la terre est plate. Mais elle est ronde et a donc une courbure qui vient contrarier notre représentation: se contenter de mettre de côté la taille des objets sur Terre ne suffit plus pour la représenter. Il faut donc trouver une méthode pour aplatir la réalité, pour qu’elle rentre en deux dimensions. On appelle celà une projection géographique:
Formule qui a une longitude/latitude sur la Terre va donner une coordonnées X, Y sur un plan.
Pour cela, on a recours à deux étapes.
1è étape: trouver une forme pour la Terre
La première étape consiste à définir une forme pour la Terre, il s’agit de la modéliser. On doit simplifier certaines de ses caractéristiques pour en avoir un modèle utilisable. Deux éléments seront simplifiés:
- La forme à la surface
- La forme générale.
La terre n’est pas statique, sa surface bouge en fonction des vents, les océans sont soumis aux marées. On va fixer ces éléments en une représentation statique, immobile, de référence, qu’on appelle géoïde. On la définit en considérant la forme qu’auraient les océans s’ils n’étaient soumis qu’à l’attraction de la Terre et à sa rotation, et on étend de manière similaire la définition aux continents. On se retrouve alors avec une sorte de boule toute lisse mais très irrégulière.
Cette boule qu’est notre géoïde n’en est en fait pas une: la Terre est ronde, mais elle n’est pas parfaitement ronde. Elle est un peu aplatie au niveau des pôles par exemple, on peut l’appeler “patatoïde” pour désigner une forme plus ou moins ronde. On a cependant besoin d’un modèle pour pouvoir effectuer nos calculs dessus, il faut donc trouver une forme régulière sur laquelle on pourra s’appuyer. Une fois la forme sélectionnée, ses dimensions seront celles qui colleront le mieux à notre géoïde.
Le premier modèle et le plus simple est de considérer une sphère. On a vu que ce modèle n’était pas le bon puisque la Terre est aplatie au pôle. Pour créer une sphère de rayon R, on prend un cercle de Rayon R qu’on fait tourner autour d’un de ses diamètres.
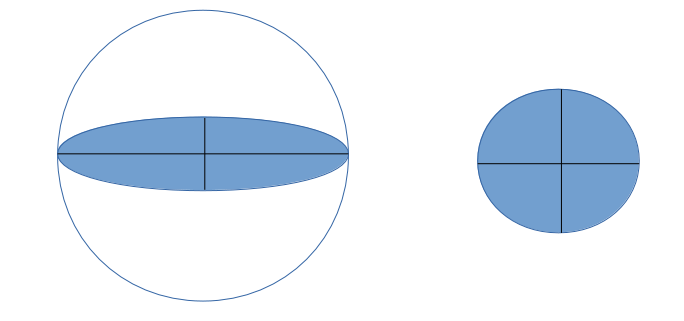
Plus proche est ce qu’on appelle un ellipsoïde. Avec cet ellipsoïde, on a bien une sphère aplatie aux pôles.
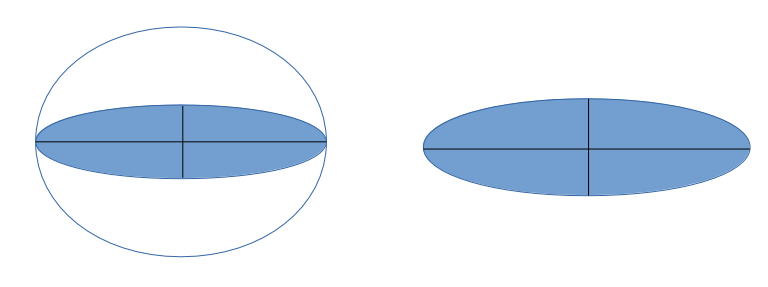
Pour créer un ellipsoïde, on utilise une ellipse qu’on fait tourner autour de son grand axe. Ainsi, pour caractériser un ellipsoïde, on se contente de donner les dimensions de son grand axe et de son petit axe, c’est suffisant pour savoir de quoi on parle. On en donne généralement le demi-grand axe et le demi-petit axe.
Quelques exemples d’ellipsoïdes
| Nom | Demi Grand Axe | Demi Petit Axe |
|---|
On a un ellipsoïde qu’on va utiliser pour modéliser notre Terre, le géoïde. Il faut maintenant décider de comment les placer l’une par rapport à l’autre. On peut décider de faire coïncider leurs centres et leurs axes, mais il est possible aussi qu’il y ait des décalages pour que les deux formes se superposent plus exactement.
On appelle datum la donnée d’un ellipsoïde, la position de son centre ainsi que l’orientation de ses axes. Au lieu de la position de son centre on peut aussi donner le point où le géoïde et l’ellipsoïde sont tangents, leur point commun à la surface du globe. On l’appelle le point fondamental.
Deux exemples de datum basés sur les ellipsoïdes qu’on a déjà rencontré:
- Nouvelle Triangulation de la France: utilisée par l’IGN jusqu’à récemment, elle se base sur l’ellipsoïde Clarke 1880 IGN, et son point de rencontre avec le géoïde (point fondamental) est le Panthéon à Paris.
- WGS84: basé sur l’ellipsoïde du même nom, il est utilisé dans le système GPS actuel.
2è étape: Projeter en 2-dimensions
On se retrouve à présent avec une modélisation de la Terre par un ellipsoïde ayant une position bien précise dans l’espace ainsi qu’une orientation. On va maintenant chercher une méthode pour que chaque point de l’ellipsoïde puisse se retrouver sur un espace en 2 dimensions. On veut projeter notre sphère sur une surface plane.
On peut imaginer que la sphère rayonne comme une ampoule électrique et qu’on y place du papier photographique autour. Ce papier photographique est ensuite récupéré avec l’image que la Terre a projeté dessus et devient alors notre carte. Mais quelle forme a ce papier photographique ? Il y a trois façons de faire:
- Projection conique
- Projection cylindrique
- Projection azimutale
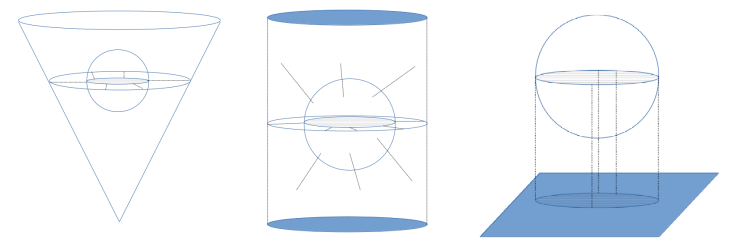
Selon que le papier photographique est un cylindre, un cône ou un plan. On a choisi ces surfaces parce qu’elles sont dites développables, on peut par exemple étaler un cylindre sur un plan sans déformation de sa surface, en le découpant et en le déroulant. La sphère n’est pas une surface développable, sinon on ne se créerait pas toutes ces difficultés.
Pour chaque type de projection, on peut placer la surface développable différemment, créant ainsi de multiples projections.
Le choix d’une projection dépend de l’utilisation finale de la carte:
- Cherche-t-on à conserver les formes ou les surfaces ?
- A quel endroit se trouve la zone que l’on souhaite cartographier ?
- Est-on plutôt proche des pôles ou des équateurs ?
Selon les réponses à ces différentes questions, une projection va être choisie plutôt qu’une autre. En effet, il n’y a pas une projection qui va posséder toutes ces propriétés.
Les projections qui conservent les surfaces sont dites équivalentes.
Les projections qui conservent les angles (et donc les formes) sont dites conformes. Un cap, un virage sur la carte sera le même en réalité.
Une projection ne peut pas être à la fois conforme et équivalente.
Quelques exemples de projections
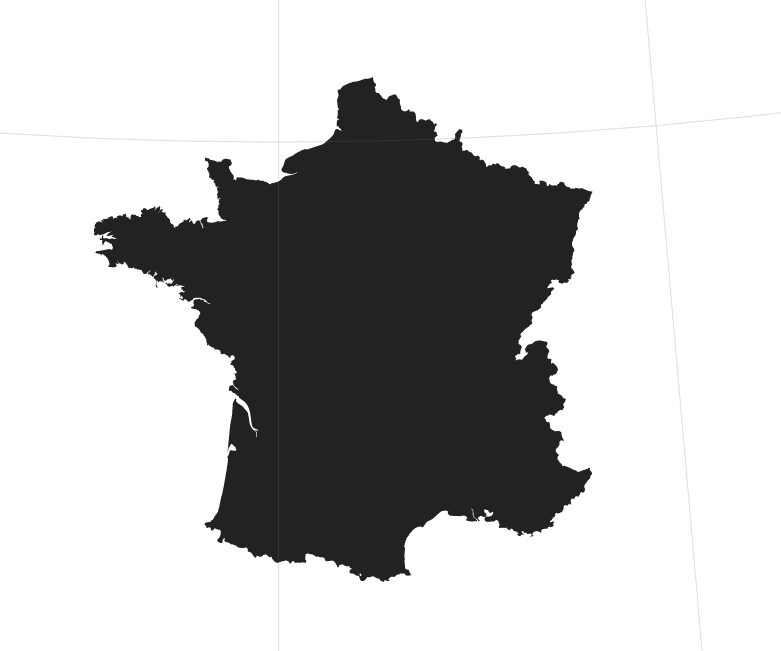
Projection conique de Lambert
Il s’agit d’une projection conique, ainsi les méridiens convergent tous vers un point unique et le pôle sud prend toute la place en bas de la carte.
Elle préserve les angles, ainsi elle fut utilisée par l’artillerie française pendant la guerre 14-18: l’angle de tir en réalité est le même que l’angle de tir sur la carte.
C’est la projection officielle pour la france:
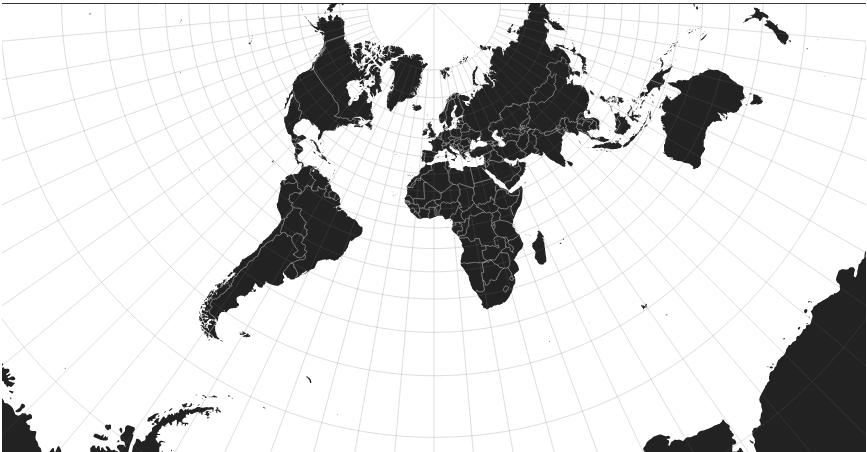
Projection de Mercator
Il s’agit d’une projection cylindrique, dont le cylindre touche la Terre à l’équateur.

Comme la projection de Lambert, elle conserve les angles et les formes. C’est ainsi la projection utilisée majoritairement pour la navigation, puisque les caps sur la carte sont les mêmes qu’en réalité.
En revanche, les pôles présentent des distorsions très importantes en surface. Le Groënland a ainsi une surface comparable à celle de l’Afrique alors qu’il est en réalité 14 fois plus petit, et l’antarctique semble aussi grande que tout le reste des terres émergées.
C’est cette projection, à quelques détails près, qui est utilisée pour les cartes en lignes telles que Google Maps. Les cartes en ligne utilisent la projection dite Web Mercator, qui coïncide avec Mercator à petite échelle (peu zoomée, carte du monde), mais utilise une sphère au lieu d’un ellipsoïde pour les grandes échelles (très zoomée, carte de rue).
Projection de Gall-Peters
La projection de Gall-Peters presèrve les surfaces, on dit qu’elle est équivalente. C’est une projection cylindrique.

Ainsi les surfaces représentées sont proches de la réalité et permettent de mieux visualiser les superficies réelles des différentes pays/continents. Ainsi, on peut comparer le groenland et l’afrique, qui sont de superficie très différente, ce que la projection Mercator ne rend pas.
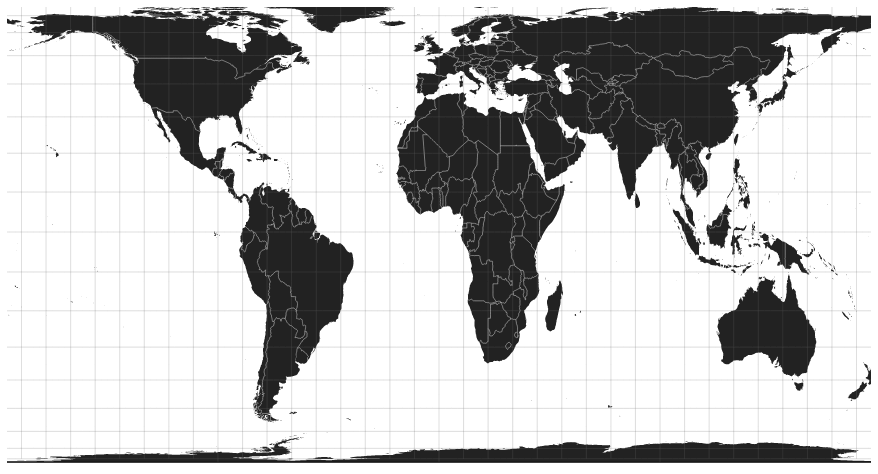
En revanche, Gall-Peters présente de fortes distorsions de formes.
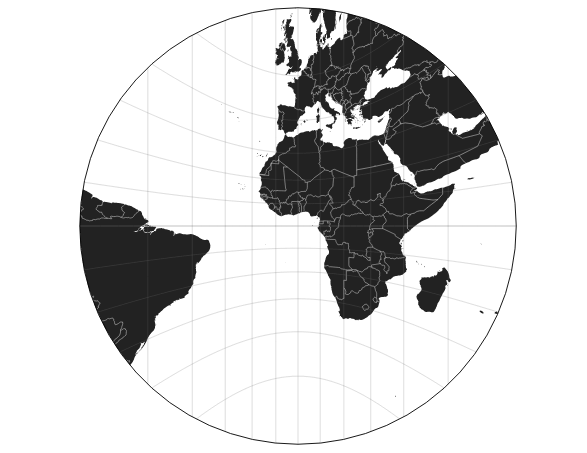
Projection Gnomonique
La dernière projection présentée est une projection azimutale, c’est à dire la projection de la sphère sur un plan.
Cette projection transforme les grands cercles en droites, ainsi les trajectoires circulaires comme celles des météorites apparaissent rectilignes.
Une autre propriété intéressante est que le chemin le plus court sur une sphère étant un arc de cercle, ce sont des droites sur les cartes gnomoniques. Ce n’est pas le cas sur les autres projections, ainsi les trajectoires des avions paraissent incurvées quand elles sont représentées sur une projection différente alors qu’ils vont en réalité au plus court.
Récapitulatif
Ainsi on a vu que pour visualiser des données géographiques sur une surface 2D, on a besoin de choisir soi-même une projection, à savoir un datum (ellipsoïde + sa position par rapport à la Terre) et une projection.
Mercator est la projection la plus communément utilisée, mais il peut être utile d’en considérer d’autres:
La radiogoniométrie, qui calcule la direction d’arrivée des ondes radios, utilise la projection goniométrique pour représenter les trajectoires.
Les sciences politiques peuvent utiliser une projection équivalente pour mieux apprécier les superficies des différents pays.
Les différentes projections vues dans ce chapitre sont regroupées dans le tableau suivant.
| Nom | Surface développable | Type | Conserve | Remarque |
|---|
Il existe des projections plus exotiques utilisant d’autres surfaces que les trois citées ci-dessus, on en recense plus de 200.
